La soluzione del paradosso dei gemelli
Il paradosso dei gemelli è un esperimento mentale elaborto da Herbert Dingle per confutare la teoria della relatività di Einstein.
Cosa afferma il paradosso dei gemelli? Un gemello parte per un viaggio nello spazio, raggiunge una stella a 10 anni luce e torna sulla Terra. Quando raggiunge la stella, quale anno è sulla Terra? Inoltre, quando l'astronauta torna sulla Terra è più giovane o più vecchio di suo fratello gemello?
Alcune incoerenze logiche del paradosso
La teoria della relatività elimina il concetto di simultaneità degli eventi. Non si può affermare che due eventi sono simultanei se si verificano in uno spazio-tempo differente.
Quando osserviamo qualcosa molto lontano, stiamo guardando la luce originata da quegli eventi in un remoto passato e ci troviamo in uno spazio-tempo diverso.
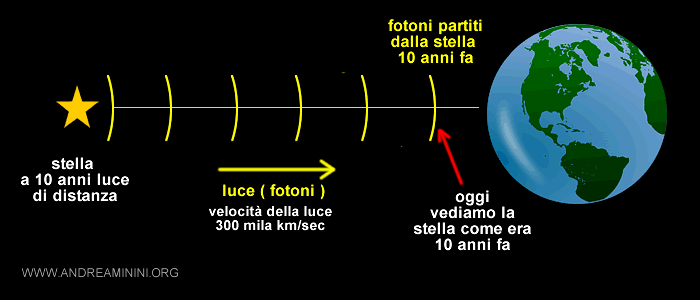
La velocità della luce viaggia a 299.792 km/sec.
Esempio. Se osservo una stella situata a 10 anni luce di distanza dalla Terra, sto guardando l'immagine passata della stella com'era 10 anni fa. La stella non si trova nemmeno più là. Potrebbe anche non esistere più. Gli eventi non possono essere mai simultanei a queste distanze.
L'astronave non è un sistema inerziale ma accelerato
Inoltre, l'astronave non è propriamente un sistema inerziale bensì un sistema accelerato, perché per raggiungere la velocità di viaggio deve accelerare ( tratto rosso ) e poi decelerare ( tratto blu ) in prossimità della stella, poi nuovamente accelerare e decelerare per tornare sulla Terra.
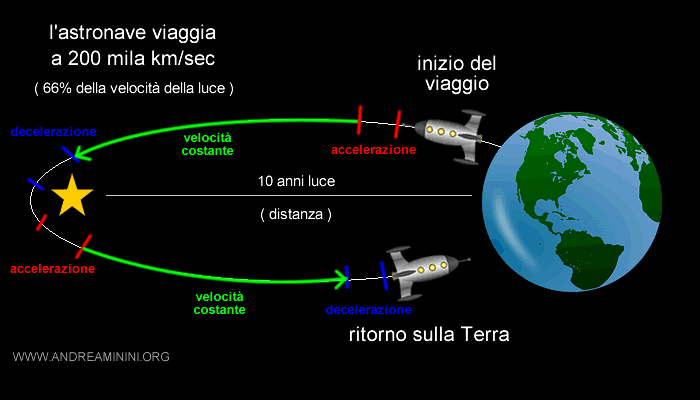
Soltanto nel tragitto intermedio ( tratto verde ) l'astronave viaggia a velocità costante ed è un sistema inerziale.
Se l'astronave è un sistema accelerato, allora non può essere applicata la teoria della relatività ristretta perché quest'ultima si applica soltanto ai sistemi inerziali.
All'astronave andrebbe applicata la teoria della relatività generale che estende la relatività a tutti i sistemi, sia inerziali che accelerati.
Nota. La teoria della relatività generale conferma i risultati di Einstein.
L'andata e il ritorno sono due sistemi inerziali diversi
Se per semplicità tralascio le fasi di accelerazione-decelerazione, l'andata e il ritorno dell'astronave restano comunque due sistemi inerziali diversi e vanno analizzati in modo a se stante.
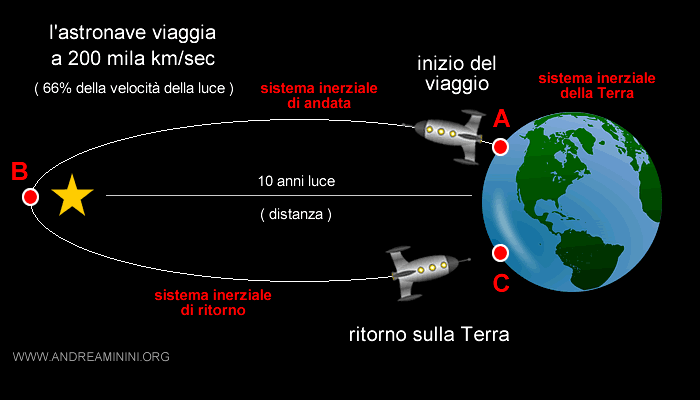
Ci sono tre sistemi inerziali da considerare e non più due:
- Il sistema inerziale della Terra
- Il sistema inerziale dell'astronave nel viaggio di andata ( tratto AB )
- Il sistema inerziale dell'astronave nel viaggio di ritorno ( tratto BC )
Per capire le differenze occorre approfondire la conoscenza dell'effetto Doppler relativistico.
Nota. Nel paradosso dei gemelli sono considerati solo due sistemi. Il tratto AB+BC viene considerato erroneamente come un unico sistema.
L'effetto Doppler relativistico
Nel viaggio di andata l'astronave si allontana dalla Terra a 200 mila km/sec. Quando l'astronauta guarda dietro, in direzione della Terra, sta osservando il passato della Terra.
Inoltre, ai suoi occhi il tempo sulla Terra scorre in modo diverso nella fase di andata e di ritorno. Si tratta dell'effetto Doppler relativistico.
Nella fase di andata si allontana dalla Terra e vede scorrere il tempo più lentamente sul pianeta perché viene raggiunto dai fotoni che viaggiano a 300 mila km/sec ma l'astronave viaggia nella stessa direzione della luce a 200 mila km/sec.
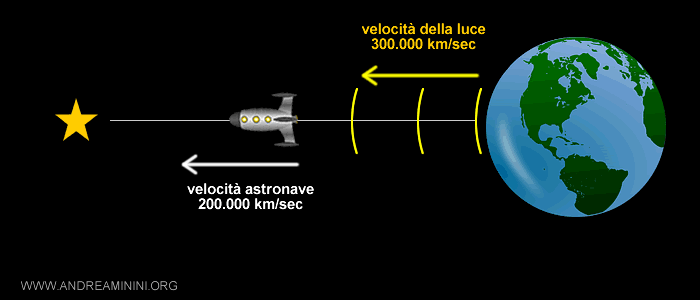
Nel viaggio di ritorno, invece, si avvicina alla Terra a 200 mila km/sec. Va incontro ai fotoni della luce provenienti dal nostro pianeta, li incontra più di frequente e vede scorrere il tempo sulla Terra più rapidamente.
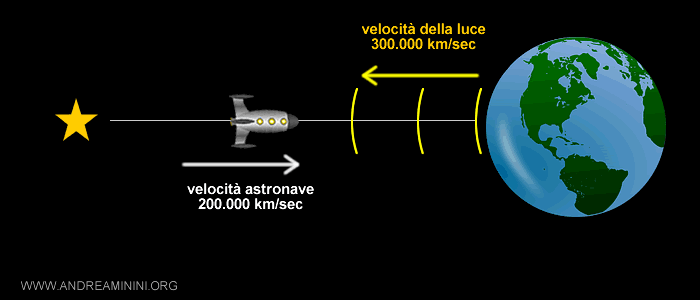
Nota. Nel viaggio di andata vede scorrere lentamente il tempo sulla Terra. Per questo motivo quando giunge sulla stella vede una data passata sulla Terra rispetto alla sua. Nel viaggio di ritorno lo vede scorrere più veloce, fino a compensare il ritardo iniziale e superare la data sull'astronave. Quando torna sulla Terra sono passati comunque 30 anni terrestri e 22 anni sull'astronave.
Qual è l'evento simultaneo all'arrivo sulla stella?
Dal punto di vista della Terra il viaggio dura trenta anni. Quindi, se l'astronave è partita nell'anno 3000, l'arrivo sulla stella ( punto B ) è previsto nell'anno 3015 terrestre ( punto D ).
Poiché il tempo rallenta alle velocità elevate, quando l'astronave arriva il suo calendario segna il 3011'. Sulla Terra dovrebbe essere il 3015 ma è veramente così?
Per capire meglio la questione è utile rappresentare graficamente i due sistemi spazio-temporali in un diagramma cartesiano, detto diagramma di Minkowski. Il diagramma nero mostra lo spazio-tempo terrestre mentre quello blu lo spazio tempo dell'astronave nella fase di andata.
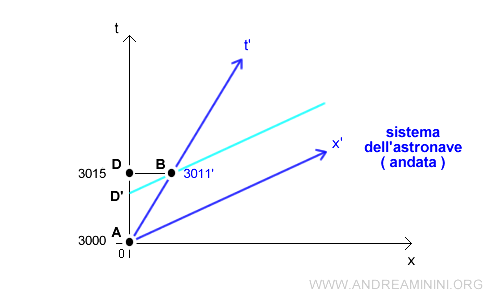
Tuttavia, i due eventi B e D non sono simultanei. Se l'astronauta osservasse la Terra vedrebbe il calendario terrestre a D' ossia a una data passata. Ad esempio, vedrebbe il 3008 terrestre (D') mentre sull'astronave è il 3011' (B).
Quando l'astronave si rimette in moto per tornare sulla Terra occorre utilizzare un altro sistema di riferimento, quello dello spazio tempo dell'astronave nel viaggio di ritorno ( diagramma rosso ).
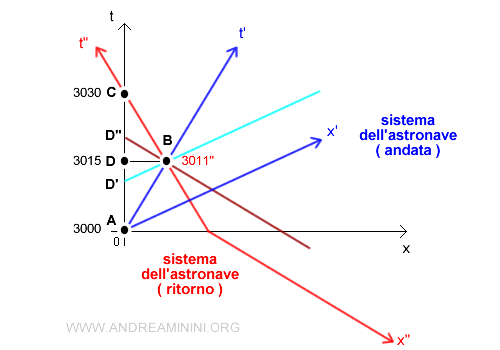
Durante il viaggio di ritorno l'astronave incontra la luce proveniente dalla Terra con maggiore frequenza. Ai suoi occhi il tempo sulla Terra comincia a scorrere velocemente.
Se guardasse la Terra vedrebbe il calendario segnare una data futura pari a D". Ad esempio, vede i calendari terrestri al 3018 (D") mentre sull'astronave è sempre il 3011" (B).
La soluzione del paradosso e il diagramma di Minkowski
In conclusione, non è possibile affermare in assoluto l'evento terrestre simultaneo ( D, D' o D" ) all'evento B poiché dipende dal sistema di riferimento.
Tuttavia, indipendentemente dal sistema di riferimento prescelto, in tutti i casi il viaggio dell'astronave dura trent'anni terrestri e l'astronauta torna sulla Terra quando il calendario segna l'anno 3030.
Il paradosso dei gemelli è stato così risolto. E' il gemello terrestre ad essere invecchiato di più ( 30 anni ) mentre il gemello astronauta di meno ( 22 anni ).
