Teorema di Jackson
La distribuzione di probabilità a regime di una rete di code aperta esiste, se le equazioni di traffico soddisfano le condizioni di stabilità in ogni singolo nodo $$ λ_i = λ_i^{in} + \sum_{j=1}^n r_{ij} \cdot λ_i < m_i \cdot μ_i $$ per ogni i=1,...,n
Se le condizioni di stabilità sono soddisfatte, la rete aperta è uguale a una catena di Markov a tempo continuo.
Pertanto, la distribuzione di probabilità a regime è
$$ π_1(x_1) \cdot π_2(x_2) \cdot \cdot \cdot π_n(x_n) $$
La distribuzione di probabilità a regime delle code corrisponde al prodotto delle distribuzioni di probabilità dei singoli nodi della rete.
Nota. Il teorema di Jackson permette di semplificare l'analisi della rete di code aperta, perché analizza ogni singolo nodo che la compone. Se ogni nodo rispetta le condizioni di stabilità, allora anche la rete è stabile.
Un esempio pratico
Una rete di code aperta è composta da due code M/M/1 in serie.
Si tratta di una rete tandem.
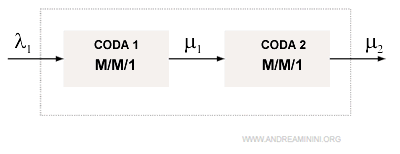
Ogni coda della rete è un nodo a cui è associato una variabile di stato x che indica il numero dei clienti nella coda.
Pertanto, lo stato del sistema è composto da due variabili di stato x1 e x2
$$ x = (x_1, x_2) $$
Nel sistema possono verificarsi tre eventi
$$ E = (a, p_1, p_2) $$
Dove a è l'arrivo di un cliente dall'esterno, p1 è l'uscita di un cliente dalla prima coda, p2 è l'uscita di un cliente dalla seconda coda.
La distribuzione degli arrivi e delle uscite è una distribuzione di Poisson, quindi i processi sono indipendenti e posso rappresentare la rete come una catena di Markov.
Il diagramma delle transizioni possibili è il seguente:
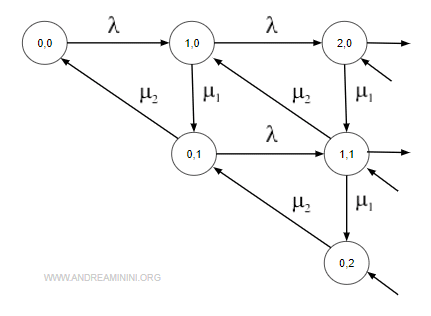
Nota. In ogni nodo è presente la coppia (x1,x2) che indica lo stato del sistema.
Il flusso di ogni nodo deve essere bilanciato, ossia gli ingressi devono coincidere con le uscite.
Ad esempio, il primo nodo (0,0) ha la seguente equazione di traffico
$$ μ_2 \cdot π(0,1) = λ \cdot π(0,0) $$
Il membro di sinistra dell'equazioni sono le transizioni che determinano l'entrata nel nodo (0,0). Nel diagramma seguente le evidenzio in rosso.
Il membro di destra sono le transizioni in uscita dal nodo (0,0) che nel diagramma evidenzio in blu.
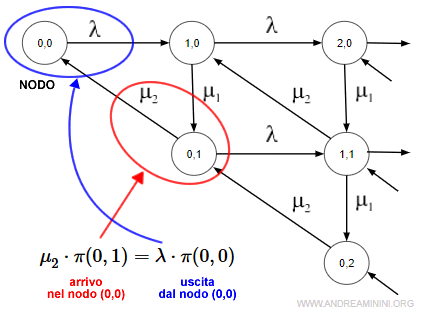
Nota. Nel caso nel nodo (0,0) ci sono solo due transizioni, una in uscita e l'altra in entrata. La transizione in uscita (blu) fa transitare il sistema dallo stato (0,0) allo stato (1,0). La transizione in entrata (rossa) fa transitare il sistema dallo stato (0,1) allo stato (0,0). Negli altri nodi della rete (stati del sistema) le transizioni in uscita e in entrata possono essere più di due.
Se l'equazione è bilanciata diventa
$$ μ_2 \cdot π(0,1) - λ \cdot π(0,0) = 0 $$
Più in generale l'equazione del traffico di un nodo qualsiasi è$$ λ \cdot π (x_1-1,x_2) + μ_1 \cdot π(x_1+1,x_2-1) + μ_2 \cdot π(x_1,x_2+1) = \\ = λ \cdot π (x_1,x_2) + μ_1 \cdot π(x_1,x_2) + μ_2 \cdot π(x_1,x_2) $$ che quando il flusso è bilanciato diventa $$ λ \cdot π (x_1-1,x_2) + μ_1 \cdot π(x_1+1,x_2-1) + μ_2 \cdot π(x_1,x_2+1) \\ - λ \cdot π (x_1,x_2) - μ_1 \cdot π(x_1,x_2) - μ_2 \cdot π(x_1,x_2) = 0 $$
Nel secondo nodo (1,0) gli stati delle code sono x1=1 e x2=0.
L'equazione di traffico del secondo nodo (1,0) è
$$ μ_2 \cdot π(1,1) + λ \cdot π(0,0) = λ \cdot π(1,0) + μ_1 \cdot π(1,0) $$
che diventa quando il traffico è bilanciato
$$ μ_2 \cdot π(1,1) + λ \cdot π(0,0) - λ \cdot π(1,0) - μ_1 \cdot π(1,0) = 0 $$
Per ogni nodo della rete posso scrivere un'equazione del traffico e bilanciare il flusso a zero.
La somma di tutte le probabilità di transizioni è uguale a 1.
$$ \sum_{x_1} \cdot \sum_{x_2} π(x_1,x_2)= 1 $$
La probabilità di stato a regime in una catena di Markov è
$$ π(x_1,x_2) = (1- \frac{λ}{μ_1}) \cdot (1- \frac{λ}{μ_2}) \cdot ( \frac{λ}{μ_1})^{x_1} \cdot ( \frac{λ}{μ_2})^{x_2} $$
Considerando che il carico λ/μ1 e λ/μ2 sono i coefficienti di carico della prima e della seconda coda
$$ δ_1 = \frac{λ}{μ_1} $$
$$ δ_2 = \frac{λ}{μ_2} $$
posso riscrivere le probabilità di stato a regime della rete
$$ π(x_1,x_2) = (1- δ_1) \cdot (1- δ_2) \cdot δ_1^{x_1} \cdot δ_2^{x_2} $$
Pertanto, la probabilità di stato a regime della rete di code è uguale al prodotto delle probabilità di stato a regime delle singole code.
$$ π(x_1,x_2) = [ (1- δ_1) \cdot δ_1^{x_1} ] \cdot [ (1- δ_2) \cdot δ_2^{x_2} ] $$
Nota. Considerando singolarmente la coda 1 la sua probabilità di stato a regime è $$ π(x_1) = (1- δ_1) \cdot δ_1^{x_1} = (1- \frac{λ}{μ_1}) \cdot ( \frac{λ}{μ_1})^{x_1} $$ Lo stesso vale per la coda 2. $$ π(x_2) = (1- δ_2) \cdot δ_2^{x_2} = (1- \frac{λ}{μ_2}) \cdot ( \frac{λ}{μ_2})^{x_2} $$
E così via.
