L'unione di sottospazi vettoriali

L'unione di due sottospazi vettoriali non è un sottospazio vettoriale.

Sia V uno spazio vettoriale nel campo K e siano A e B due sottospazi vettoriali di V. L'unione dei sottospazi A ∪ B non è in generale un sottospazio vettoriale.

Perché?

L'unione A ∪ B non è chiuso alla somma.

$$ a+b \notin A \cup B $$

E' chiuso soltanto al prodotto scalare.

$$ k \cdot a \in A \cup B $$

La dimostrazione

Dati due sottospazi vettoriali A e B, devo dimostrare se l'unione A ∪ B è un sottospazio vettoriale.

$$ A \cup B $$

Secondo la prima proprietà dei sottospazi, dati due vettori generici a e b dell'insieme A U B, anche la somma a+b appartiene a A U B.

$$ \forall \ \vec{a} \in A , \vec{b} \in B ⇒ \vec{a}+\vec{b} \in A \cup B $$

Questo però non è sempre vero.

Quindi, la proposizione è falsa.

Un esempio pratico

Sia V lo spazio vettoriale R².

Ad esempio, il piano a due dimensioni x,y è composto da R·R punti ( R² ).

E' un esempio pratico di spazio vettoriale R².

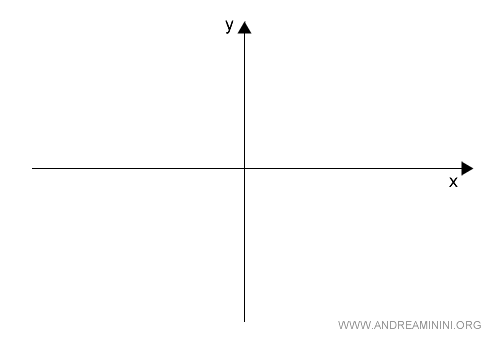
Prendo in considerazione due sottospazi vettoriali X e Y.

Ad esempio, l'asse x e l'asse y.

$$ X = \{ \binom x y \in R^2, y=0 \} $$

$$ Y = \{ \binom x y \in R^2, x=0 \} $$

Gli assi X e Y sono entrambi sottospazi vettoriali del piano V perché sono sistemi lineari omogenei.

Nota. essendo sottospazi di dimensione 1 agevolano anche la rappresentazione grafica, rendendo più comprensibile la spiegazione dei concetti.

L'unione X∪Y è l'insieme dei vettori sull'asse X e sull'asse Y ( blu ).

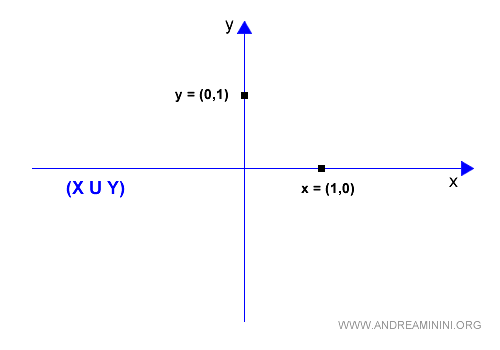
L'unione X∪Y non è un sottospazio vettoriale perché non è sempre chiuso rispetto alla somma di due elementi generici x+y.

Per dimostrarlo ricorro a un controesempio.

Prendo due vettori

$$ \vec{x} \in X $$

$$ \vec{y} \in Y $$

Ad esempio

$$ \vec{x}=\begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \vec{y}=\begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

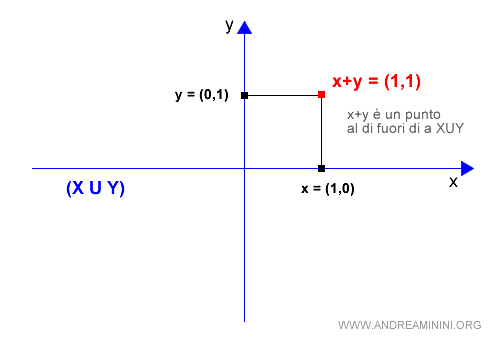
Poi li sommo x+y.

La somma è uguale a x+y

$$ \vec{x}+\vec{y} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$

Ora devo verificare se la somma dei due vettoriali è inclusa nell'unione X∪Y perché è una delle due proprietà dei sottospazi vettoriali.

$$ \vec{x}+\vec{y} \in X \cup Y $$

E' subito evidente geometricamente che la somma dei vettori x+y non appartiene all'unione X∪Y, perché il punto (x,y)=(1,1) si trova al di fuori di entrambi gli spazi vettoriali ( asse X + asse Y ).

Sostituisco la somma x+y

$$ X = \{ \binom 1 1 \in R^2, y=0 \} $$

$$ Y = \{ \binom 1 1 \in R^2, x=0 \} $$

Quindi

$$ X = \{ \binom 1 1 \in R^2, 1=0 \} $$

$$ Y = \{ \binom 1 1 \in R^2, 1=0 \} $$

Sono entrambe non verificate ( false ).

Quindi, la somma x+y non è inclusa nell'unione X∪Y.

$$ \vec{x}+\vec{y} \notin X \cup Y $$

L'unione di due sottospazi vettoriali non soddisfa la proprietà della somma degli spazi vettoriali.

Nota. L'unione dei sottospazi vettoriali soddisfa soltanto la proprietà del prodotto scalare degli spazi vettoriali, perché kx ∈ X∪Y. Questo però non è sufficiente a definire un sottospazio vettoriale. E' necessario che entrambe le proprietà siano soddisfatte.

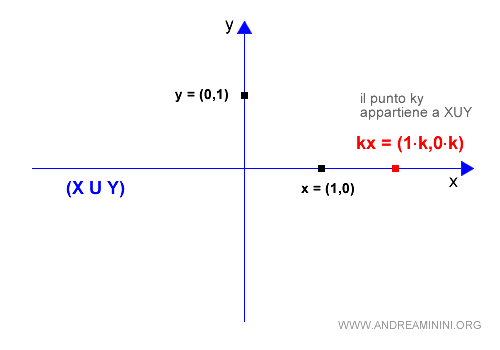
Ho così dimostrato che in generale l'unione di due sottospazi vettoriali non è un sottospazio vettoriale.

Il piu' piccolo sottospazio vettoriale che contiene l'unione dei sottospazi

La somma degli spazi vettoriali A+B è il più piccolo sottospazio vettoriale di V che contiene l'unione dei sottospazi A∪B.

Dimostrazione

In uno spazio vettoriale V prendo in considerazione due sottospazi vettoriali A e B

$$ A,B \subseteq V $$

Considero un generico sottospazio vettoriale L che contiene A e B, ossia l'unione dei due sottospazi A∪B.

$$ A \cup B \subseteq L \subseteq V $$

Essendo L un sottospazio vettoriale, per la definizione di sottospazio, contiene al suo interno la somma dei vettori appartenenti a L.

Di conseguenza, anche la somma dei vettori di A e B

$$ \{ \vec{a}+\vec{b} \ | \ \vec{a} \in A \ , \ \vec{b} \in B \} \subseteq L $$

Quindi, il sottospazio vettoriale L contiene al suo interno la somma dei sottospazi vettoriali A+B

$$ A+B \subseteq L $$

In generale, qualsiasi sottospazio vettoriale che contiene A e B include al suo interno anche la somma A+B.

La somma dei sottospazi vettoriali A+B è a sua volta un sottospazio vettoriale (vedi dimostrazione).

Pertanto, fra tutti i sottospazi vettoriali che contengono l'unione dei sottospazi A∪B, il sottospazio somma A+B è il più piccolo.

Spiegazione. Il sottospazio A+B è contenuto in tutti i sottospazi che contengono A e B, ossia l'unione A∪B. Di conseguenza A+B è sicuramente il più piccolo tra tutti i sottospazi vettoriali di V che contengono l'unione dei sottospazi A∪B.

Osservazioni

Alcune osservazioni sull'unione dei sottospazi vettoriali

• In generale l'unione di due sottospazi vettoriali non è un sottospazio vettoriale. Tuttavia, può capitare in alcuni casi particolari che anche l'unione dei sottospazi vettoriali sia un sottospazio vettoriale. Ad esempio, se uno dei sottospazi vettoriali è contenuto nell'altro $$ X \subset Y $$ anche l'unione è un sottospazio vettoriale perché coincide con il sottospazio Y. $$ X \cup Y = Y $$

E così via.