L'intersezione dei sottospazi vettoriali
L'intersezione di due sottospazi vettoriali è un sottospazio vettoriale.
Sia V uno spazio vettoriale sul campo K e siano A e B due sottospazi vettoriali di V. L'intersezione A⋂B è un sottospazio di V.
La dimostrazione
Prendo in conserazione uno spazio vettoriale V e due sottospazi vettoriali A e B di V.
Devo dimostrare che anche l'intersezione dei sottospazi vettoriali A⋂B è uno sottospazio vettoriale.
Per capirlo verifico se l'intersezione soddisfa tutte le proprietà dei sottospazi vettoriali.
Nota. Un sottospazio vettoriale deve contenere il vettore nullo ed essere chiuso alle operazioni di addizione e moltiplicazione per uno scalare.
1) Presenza dell'elemento nullo
Il vettore nullo è presente in entrambi sia in A che in B.
$$ \vec{0} \in A $$
$$ \vec{0} \in B $$
Quindi il vettore nullo appartiene all'intersezione di A⋂B
$$ \vec{0} \in A⋂B $$
Pertanto, non posso escludere che l'intersezione A⋂B sia un sottospazio vettoriale.
Devo procedere e verificare anche le altre proprietà dei sottospazi vettoriali.
2) Chiusura rispetto alla somma di due vettori
Prendo due vettori qualsiasi appartenenti all'intersezione dei due sottospazi A⋂B
$$ \vec{a},\vec{b} \in A⋂B $$
I due vettori a e b appartengono a entrambi i sottospazi A e B perché sono tratti dall'intersezione A⋂B
$$ \vec{a},\vec{b} \in A $$
$$ \vec{a},\vec{b} \in B $$
Essendo A e B due sottospazi vettoriali, sono chiusi rispetto alla somma e al prodotto.
Pertanto, la somma dei vettori a e b appartiene al sottospazio vettoriale A
$$ \vec{a}+\vec{b} \in A $$
Per la stessa ragione la somma dei vettori a e b appartiene al sottospazio vettoriale B
$$ \vec{a}+\vec{b} \in B $$
La somma a+b è presente sia in A che in B
Quindi, la somma dei due vettori appartiene all'intersezione A⋂B
$$ \vec{a}+\vec{b} \in A⋂B $$
In questo modo ho dimostrato che l'intersezione di due sottospazi è chiuso rispetto alla somma.
Questa proprietà dei sottospazi vettoriali è soddisfatta.
3) Chiusura rispetto al prodotto di un vettore per uno scalare
Considero un vettore v qualsiasi appartenente all'intersezione dei due sottospazi vettoriali A⋂B
$$ \vec{v} \in A⋂B $$
Poi considero un numero scalare qualsiasi appartenente al campo K
$$ \lambda \in K $$
Il vettore v appartiene a entrambi i sottospazi vettoriali perché l'ho tratto dall'intersezione A⋂B
$$ \vec{v} \in A $$
$$ \vec{v} \in B $$
Essendo A e B dei sottospazi vettoriali, sono chiusi rispetto al prodotto di ogni vettore per uno scalare.
Quindi il prodotto del vettore v per lo scalare λ appartiene sia al sottospazio A, sia al sottospazio B
$$ \lambda \cdot \vec{v} \in A $$
$$ \lambda \cdot \vec{v} \in B $$
Pertanto, il prodotto del vettore v per lo scalare λ appartiene all'intersezione A⋂B.
Ho così dimostrato che l'intersezione A⋂B è chiusa rispetto al prodotto per uno scalare.
Questa proprietà dei sottospazi vettoriali è verificata
In conclusione
L'intersezione di due sottospazi contiene il vettore nullo ed è chiusa sia nella somma dei vettori che nel prodotto di un vettore per uno scalare. Quindi anche l'intersezione di due sottospazi A⋂B è un sottospazio vettoriale.
L'intersezione A⋂B è un sottospazio vettoriale di A e di B.
E ovviamente l'intersezione A⋂B è un sottospazio vettoriale anche dello spazio vettoriale V.
Un esempio pratico
Il piano cartesiano xy è uno spazio vettoriale V del campo K=R2.
E' un piano a due dimensioni RxR.
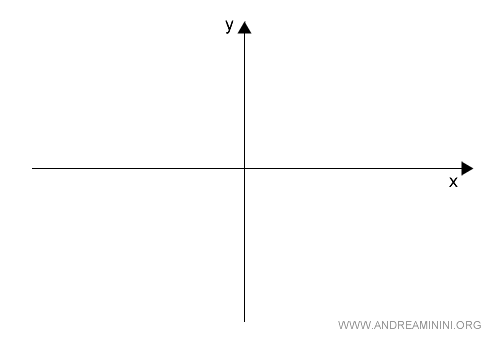
L'asse X e l'asse Y sono due sottospazi vettoriali dello spazio V.
Entrambi i sottospazi sono sistemi lineari omogenei e includono l'elemento nullo.
$$ X = \{ \binom x y \in R^2, y=0 \} $$
$$ Y = \{ \binom x y \in R^2, x=0 \} $$
L'intersezione X⋂Y degli assi cartesiani è la seguente:
$$ X \cap Y = \{ \binom x y \in R^2, x=0, y=0 \} $$
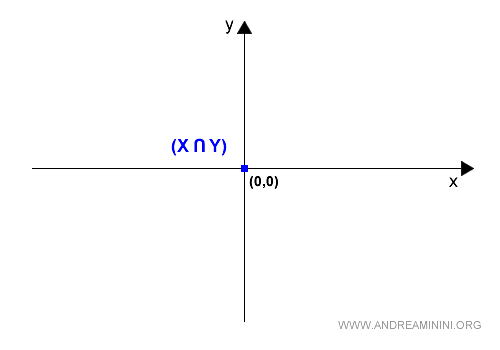
In pratica l'intersezione X⋂Y contiene al suo interno solo il vettore nullo.
$$ X \cap Y = \{ \vec{0} \} $$
Attenzione. Questo non vuol dire che l'intersezione è nulla X⋂Y=Ø. L'intersezione non è nulla X⋂Y≠Ø perché contiene al suo interno un vettore X⋂Y={0} ossia il vettore nullo.
Dal punto di vista grafico l'intersezione è il punto di origine O (blu) del diagramma cartesiano.
La presenza del vettore nullo non mi permette di escludere che X⋂Y sia uno spazio vettoriale.
Devo verificare le altre proprietà dei sottospazi vettoriali.
Proprietà 1 (chiusura rispetto alla somma dei vettori)
Considero due vettori qualsiasi dell'intersezione X⋂Y
$$ \vec{x} \in X $$
$$ \vec{y} \in Y $$
La somma dei vettori è uguale a x+y
$$ \vec{x}+\vec{y} $$
Devo capire se il vettore somma è incluso o meno nell'intersezione X⋂Y.
$$ X \cap Y = \{ \binom x y \in R^2, x=0, y=0 \} $$
L'intersezione X⋂Y contiene soltanto il vettore nullo.
$$ X \cap Y = \{ \vec{0} \}$$
Quindi i due vettori x e y sono entrambi il vettore nullo.
$$ \vec{x}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$
$$ \vec{y}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$
La somma del vettore nullo con se stesso è sempre il vettore nullo.
$$ \vec{x} + \vec{y}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0+0 \\ 0+0 \end{pmatrix} =\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$
Quindi, la somma dei vettori x+y è inclusa nell'intersezione X⋂Y.
$$ \vec{x}+\vec{y} =\begin{pmatrix} 0 \\ 0 \end{pmatrix} \in X \cap Y $$
La prima proprietà dei sottospazi vettoriali è soddisfatta.
Proprietà 2 (chiusura rispetto al prodotto di un vettore per uno scalare)
Per verificare la seconda proprietà dei sottospazi, considero uno scalare k e un vettore x dell'intersezione dei sottospazi X⋂Y.
$$ \vec{x} \in X⋂Y $$
$$ k \in R $$
Devo verificare se il prodotto del vettore per lo scalare appartiene o meno all'intersezione X⋂Y.
$$ X \cap Y = \{ \binom x y \in R^2, x=0, y=0 \} $$
L'intersezione X⋂Y contiene soltanto il vettore nullo.
$$ X \cap Y = \{ \vec{0} \}$$
Quindi, il vettore x è necessariamente il vettore nullo.
$$ \vec{x}=\begin{pmatrix} 0 \\ 0 \end{pmatrix} $$
Qualsiasi scalare k moltiplicato per il vettore nullo dà come risultato il vettore nullo stesso.
$$ k \cdot \vec{0} = k \cdot \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} k \cdot 0 \\ k \cdot 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \vec{0} $$
Pertanto, il prodotto per uno scalare appartiene all'intersezione X⋂Y.
$$ k · \vec{0} \in X⋂Y $$
Anche la seconda proprietà dei sottospazi vettoriali è soddisfatta.
In conclusione
L'intersezione degli assi X e Y è un sottospazio vettoriale.
L'intersezione X⋂Y è un sottospazio vettoriale di X e Y.
Inoltre, l'intersezione X⋂Y è anche un sottospazio dello spazio vettoriale V ossia del piano cartesiano.
Osservazioni
Alcune osservazioni sull'intersezione dei sottospazi vettoriali
- L'intersezione di due sottospazi vettoriali non può mai essere un insieme vuoto $$ X \cap Y \ne Ø $$
Dimostrazione. Essendo sottospazi vettoriali sia X che Y contengono per definizione l'elemento neutro dell'addizione ossia il vettore nullo $$ \vec{0} \in X \ , \ \vec{0} \in Y \Rightarrow \vec{0} \in X \cap Y $$ Quindi l'intersezione non potrà mai essere vuota perché almeno un vettore (il vettore nullo) vi appartiene. Quindi, può capitare che l'intesezione dei sottospazi vettoriali X⋂Y contenga solo il vettore nullo $$ X \cap Y = \{ \vec{0} \} $$ Non può invece mai accadere che l'intersezione dei sottospazi vettoriali sia un insieme vuoto $$ X \cap Y \ne Ø $$
